知っておくと便利な用語
読み順
通常は、英語の文章を読む順番。日本語は縦書きもあるからややこしい。
例えば、4×4の格子ならば次のような順番。
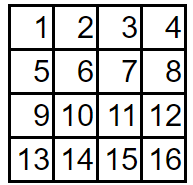
「段」と「列」
下の図で、赤の矢印の方向が「段」、青が「列」。
余談ではあるが、現実には同様に「行」と「列」で表す場合もある(数学の行列やExcelなど)が、マニュアルではすべて「段」と「列」に統一している。
数字根
ある数字のそれぞれの桁の数字を合計するという動作を、数字が一桁になるまで繰り返したときの値。
例: 98213 → 9+8+2+1+3=23 -> 2+3=5 であるから、98213の数字根は5。
次のような性質がある:
- 数字根が0になる0以上の整数は0だけ。正の整数の数字根は1~9の値になる。
- 数字を9で割ったときの値を求めると、あまりが0のときは数字根は9であり、あまりが1~8のときはその値が数字根となる。
- したがって、数字根を素早く求めるには、9で割ったときの値を求めればよい。
- 例1: 98213では、9と8+1がどちらも9の倍数であるので、足し算に含めなくても9で割ったあまりは変化しない。つまり残りの2+3=5を求めれば良い。
- 例2: 98217では、9、8+1、2+7のいずれも9の倍数であるので、9で割ったときのあまりは0である。したがって数字根は9。
mod演算
ある値を別の値で除算し、そのあまりを取得する演算。「~で割ったあまり」「~を~の範囲になるまで繰り返し~を減算する」といった表記で表されることが多い。
例: 13÷5 は2あまり3なので、13mod5は3となる。
負の数のmod演算については、モジュールによって挙動が異なるので注意する。
例1: 「-13を0~4の範囲になるまで繰り返し5を加算・減算する」という場合は、-13+3×5=2なので2である。 例2: 「-13を-4~4の範囲になるまで繰り返し5を加算・減算する」という場合は、-13+2×5=-3なので-3である。
以下のような性質が成り立つ。
- 加算・減算・乗算した結果をmodする場合、利用する数字を同じ値でmodしてから計算しても良い。
- 例1: 「(123+432-82)mod9」は、「123mod9=6」「432mod9=0」「82mod9=1」より、「6+0-1=5」となる。
- 例2: 「(3142×134)mod3」は「3142mod3=1」「134mod3=2」より「1×2=2」となる。
- 除算は利用する数字を同じ値でmodしてから計算することはできない場合がある。
- 例: 「18mod4=2」「6mod4=2」であるが、「(18÷6)mod4=3」である。
- 発展: 割る数とmodする数が互いに素である場合のみ、これは可能。「18mod5=3」「6mod5=1」であるから、「(18÷6)mod5=3」である。
アルファベットでの位置(A1Z26)
ある英字が、アルファベットで数えて何文字目であるかを数えた値。
| 文字 | 値 | 文字 | 値 | 文字 | 値 | 文字 | 値 | 文字 | 値 |
|---|---|---|---|---|---|---|---|---|---|
| A | 1 | B | 2 | C | 3 | D | 4 | E | 5 |
| F | 6 | G | 7 | H | 8 | I | 9 | J | 10 |
| K | 11 | L | 12 | M | 13 | N | 14 | O | 15 |
| P | 16 | Q | 17 | R | 18 | S | 19 | T | 20 |
| U | 21 | V | 22 | W | 23 | X | 24 | Y | 25 |
| Z | 26 |
ただし、モジュールによってはA=0、B=1…Z=25と数えるものや、Z=0、A=1…Y=25と数えるものもあるため注意。(通常はA=1、B=2…Z=26と明記されている)
n進法(二進法、十六進法、三十六進法など)
数字を表す方法の種類。普段は十進法を利用しているが、これは一の位、十の位、百の位、千の位…がそれぞれ、100、101、102、103…の個数を表していると考えることができる。
例: 31528 = 3×104 + 1×103 + 5×102 + 2×101 + 8×100
二進法では2つの数字「0」と「1」しか利用しない。そして、一の位、十の位、百の位、千の位…がそれぞれ、20、21、22、23…を表す。
例: 10110 = 1×24 + 0×23 + 1×22 + 1×21 + 0×20 = 16 + 4 + 2 = 22
同様に、n進法ではn個の数字を使って、一の位、十の位、百の位、千の位…がそれぞれ、n0、n1、n2、n3…の個数を表す、といった具合で数字を表現する。11個以上の数字を利用する場合は、英字を用いてA=11、B=12…のように利用する場合が多い。
例: 三十六進法(A=11, B=12…Z=35)で、CH3N = 12×363 + 17×362 + 3×361 + 23×360 = 559872 + 22032 + 108 + 23 = 582035
加法混色
色を混ぜて別の色を作るときの考え方の一つ(参考: ↔減法混色)。
赤、緑、青を三原色とし、それらを混ぜることによって他の色を表現する。色を加えれると明るくなり、除くと暗くなる。
色を混ぜたときの名前は以下のように表現されることが多い。